Vector addition, subtraction, and Scalar multiplication
Like numbers, you can also add and subtract vectors. But what is the meaning of adding or subtracting two vectors, and how do we do that?
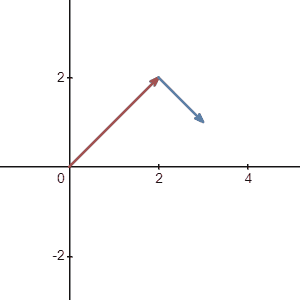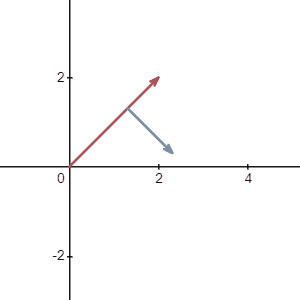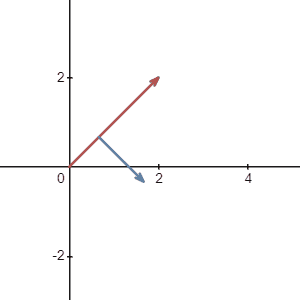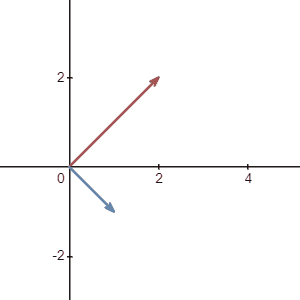
Imagine you are walking on a 2d plane and you start at the origin. Say there is a penny located at (2,2) and you are about to pick it up. So you walk to the position (2,2). Let us record this motion using vector and write this vector \(a\) as:

Then you heard someone yelling at you. The sound is coming from your right. So you walk to this person and return the penny to him unwillingly. Notice that if you look from above, the direction of this motion is Southeast because your moving direction is Northeast at the beginning. For simplicity, let say you walked exactly \(\sqrt{2}\) unit.
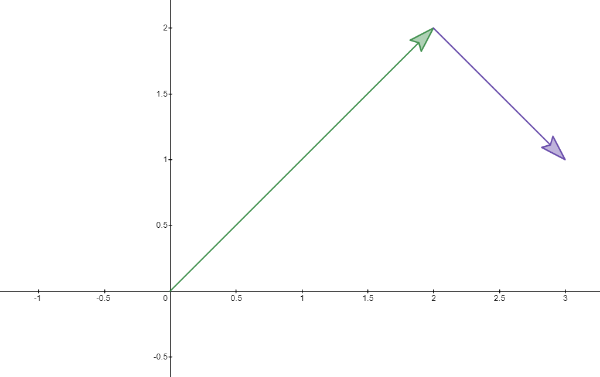
Now we need to see what is your second motion. As we learned before, moving a vector doesn’t change the vector itself, so if we move this vector and place it on the origin, we can see the tip of the vector land exactly on the point (1,-1).
So we do the same thing and record this motion using vector:
Now we can finally ask ourselves: what is the meaning of adding these two vectors \(\vec{a}\) and \(\vec{b}\)? The answer is quite straightforward. The first motion is \(\vec{a}\) and right after that you did the second motion \(\vec{b}\). If you combine these two motions and only look at the result of them, it looks like you just walked to the final point where you talked to the guy who thinks you stole his penny.
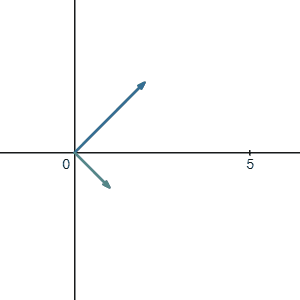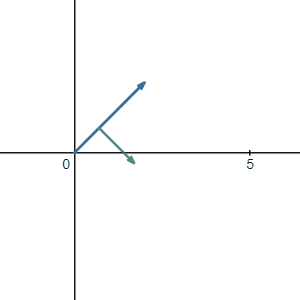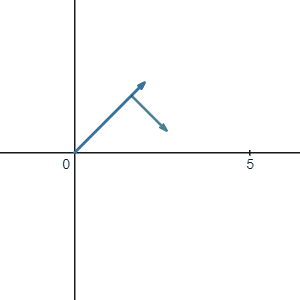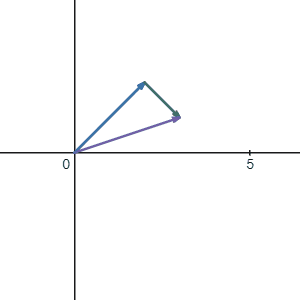
So how do we calculate the result? It is very obvious to see that the tip of \(\vec{b}\) is sitting at point (3,1). Therefore the result is just:
If you watch carefully, you can find that the x coordinate of the result is just happens to be the result of adding both x coordinate:
Same as y coordinate:
The reason is that we placed everything inside the Cartesian coordinate.
If we treat the x coordinate and the y coordinate as vectors sitting exactly on the x and y axis, then every vector can be represented as addition of those vectors!
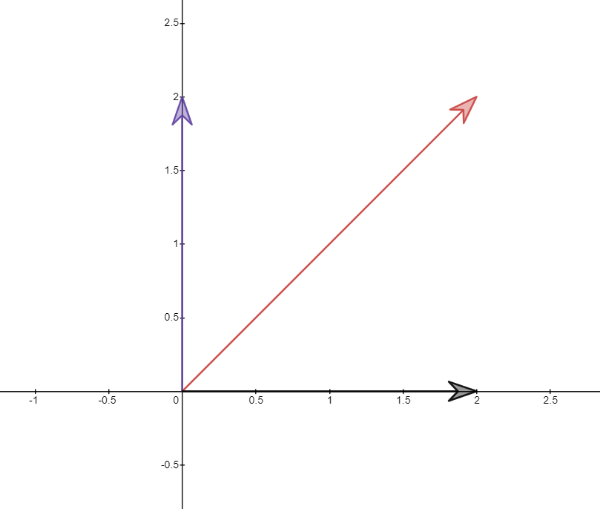
Once we realized that, we can reverse the addition and break down our \(\vec{a}\) and \(\vec{b}\). Then we add all the x direction vectors, do the same thing on y direction vectors. We will end up with two sums, one for x direction and one for y direction. So, our job is done! Because the way we write down vectors is just to write down their x and y components.
Next we are going to do some multiplication. Just like number multiplication, the multiplication is just adding the same thing many many times. Luckily, we can also do that in vector. Again, take \(\vec{a}\) from previous section as an example:
We can also multiply a negative scalar like \(-1\). Keep in mind, multiply negative values will reverse the direction of the vector.
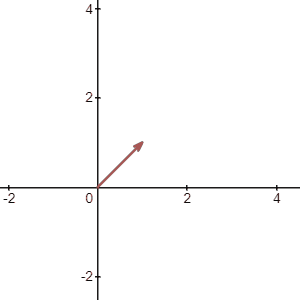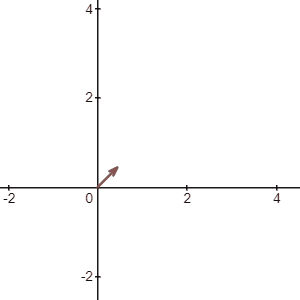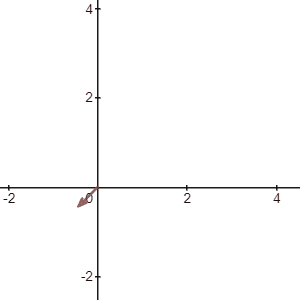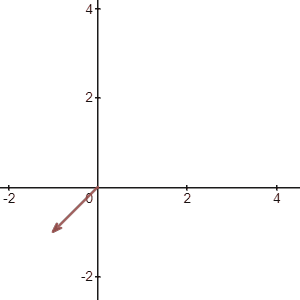
So far we know how to add any two vectors and multiply any vector with a scalar, it is a good time to introduce the subtraction.
To calculate, it is fairly easy. As you expected, instead of adding the coordinate as you did before, this time you just subtract:
To visualize it just like we did for addition, we can break down subtraction into addition and multiplication of \(-1\):
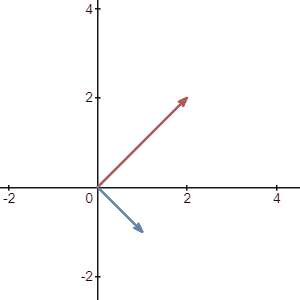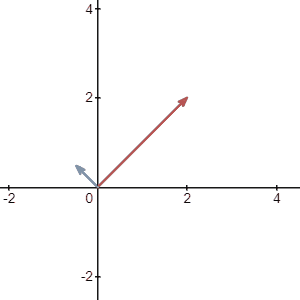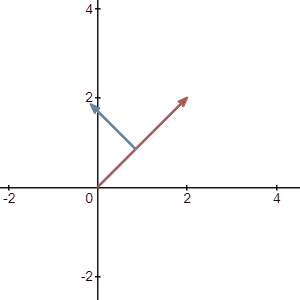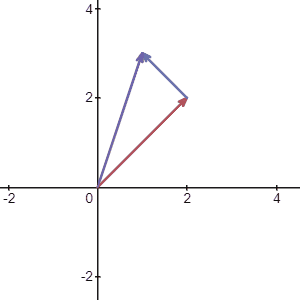
And that is the end of the first chapter!
You will see more examples and fun applications in the assignment. The addition and subtraction rules look easy but it has a huge impact on more important concepts like linear combination, span, and basis.
Now is the time to reveal the answer to the question I gave from the previous chapter: What is a vector in mathematics?
Well, mathematics people tend to have a more abstract definition. In short, a vector is the object that follows the rules of vector addition and scalar multiplication. Or you can say that vector is an element of vector space. What is a vector space? Well, we will go back to this topic. For now, you can think of vector space as a realm that has those rules we mentioned above.