What is a vector looks like?
Linear algebra begins with a simple concept in physics, more specifically mechanics: the vector. Understanding vector is the first step to understand linear algebra. To do this, we have to visit three different places, since it has different meanings in different fields.
In physics, vector is any quantity that has both direction and magnitude. For example, energy as a physical quantity is not a vector because it has no specific direction, but velocity is a vector since it has both direction(where are you going) and magnitude(how fast are you going).
In computer science, vector as a data structure has a different name called array. An array, is a data structure consisting of a collection of elements (values or variables). For example, I have many data points like 1,2,3,4,5,6,7, and I want to multiply all of them by 2. In python, we can write this as a numpy array:
import numpy as np
x = np.array(1,2,3,4,5,6,7)
and just multiply them at once:
print(2*x)
>>> [2,4,6,8,10,12,14]
But you might want to ask: What is the definition of a vector in mathematics? Take some guesses, We will reveal the answer at the end of this chapter.
In physics, a vector is usually placed in a coordinate system. For example, we can say a 2d vector called x in the Cartesian plane to be (1,1), which means that the vector is starting from the origin and pointing toward Northeast.
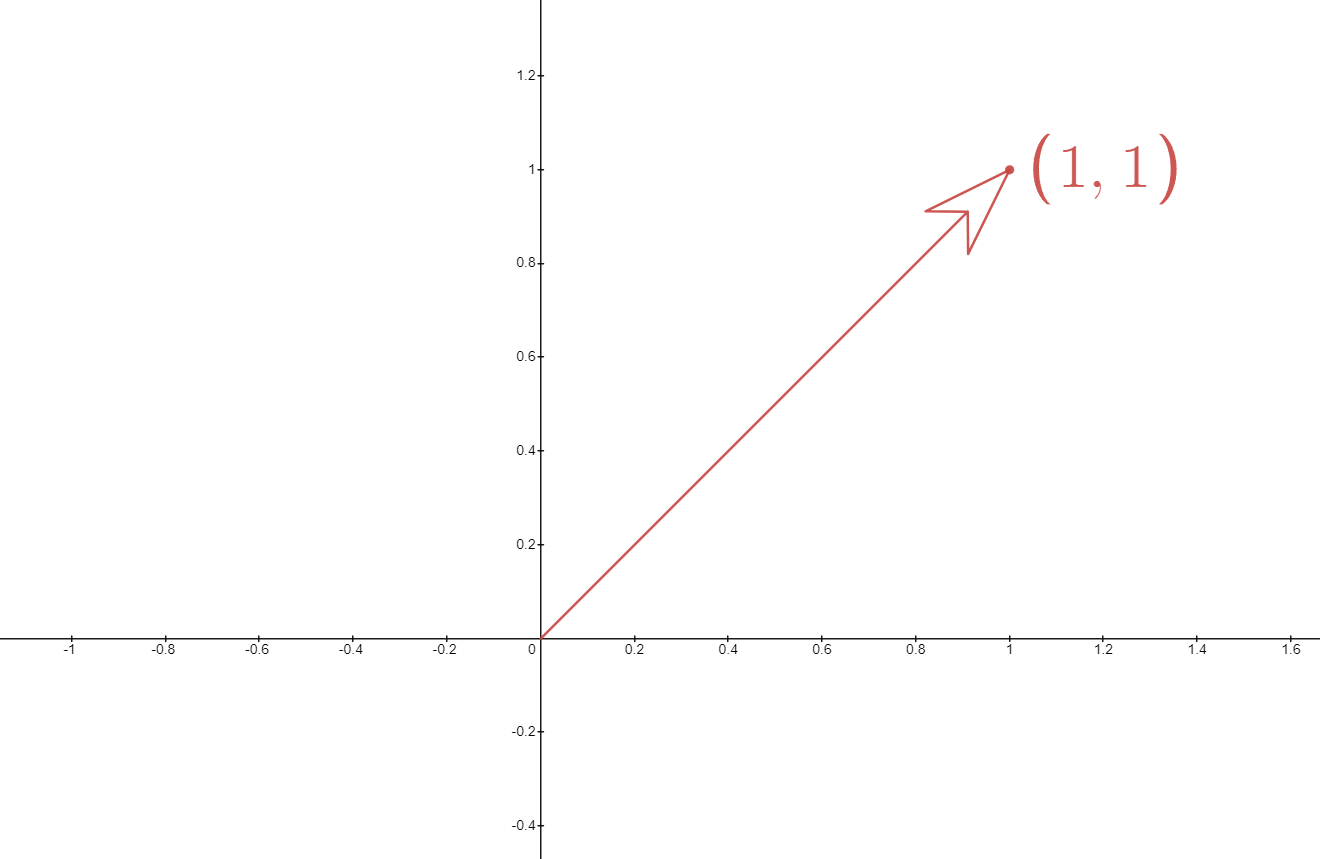
Notice that the starting point of a vector is not important, we can freely move the vector without changing it as long as it maintains the shape. The Reason is simple, changing starting point doesn’t change its direction or magnitude.
Because of that, we usually place it right on the origin and use the tip coordinate to describe the vector.
You can compute the length of this vector using Pythagorean theorem. In our case, the result is:
I put a little bar on the top of variable \(\vec{x}\) just to clarify that \(\vec{x}\) is a vector. Usually, If you don’t do that, we think the \(x\) is a Scalar. In physics, a scalar is a quantity that does not have a direction, like a number in math.
To write down the vector, we do the same thing that computer science people do: putting two or more numbers together. Once we have the vector written down, we can treat the numbers as coordinates, compute the direction and the length of the vector if we want to do that.