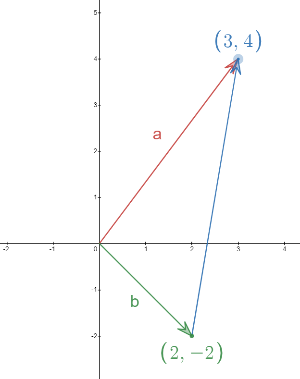
1.Two vectors \(\vec{a}\) and \(\vec{b}\) are located at the origin as showing below:
(a) Find the vector \(\vec{a}-\vec{b}\) using the vector subtraction law, and then calculate its magnitude and direction.(you can use angle to describe the direction)
(b) Without using the result from (a) and the law, find the magnitude and the direction of \(\vec{a}-\vec{b}\)
(c) compare your result from part(a) and part(b). Ask yourself which one you prefer.
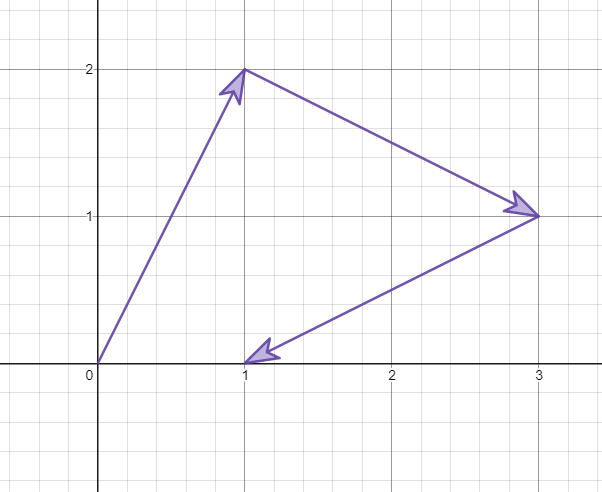
2.You are play chess on a 2d Cartesian plane. Say your knight is located at the corner of the chess board(the origin) and there is a juicy queen sitting at (6,8). Reminder: The knight’s movement is unique: it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L).

(a) Let’s assume your opponent is quite dumb, so he just don’t like to move the queen. Now how do you move your knight to kill the queen?
(b) We can use the vector notation to explain the movement of knight. For example, if we want to move the knight to (3,3), we can do:
Now, rewrite your result from (a) using vector addition and scalar multiplication.
(c) Can you proof that knight can go to any location on the chess board?
—-
Answer sheet
- Two vectors \(\vec{a}\) and \(\vec{b}\) are located at the origin as showing below:

(a) Find the vector \(\vec{a}-\vec{b}\) using the vector subtraction law, and then calculate its magnitude and direction.(you can use angle to describe the direction)
By using subtraction law, we can easily get:
We can find the magnitude using Pythagorean theorem:
To find the direction, we can use the inverse trig function:
And that is roughly East 80.5 degree North.

(b) Without using the law of vector addition and subtraction, find the magnitude and the direction of \(\vec{a}-\vec{b}\).
This time no subtraction allowed. One way we can solve this is to use the cosine law.
we began with solving the magnitude of both \(\vec{a} $ and $\vec{b}\):
Then we find the angle between them:
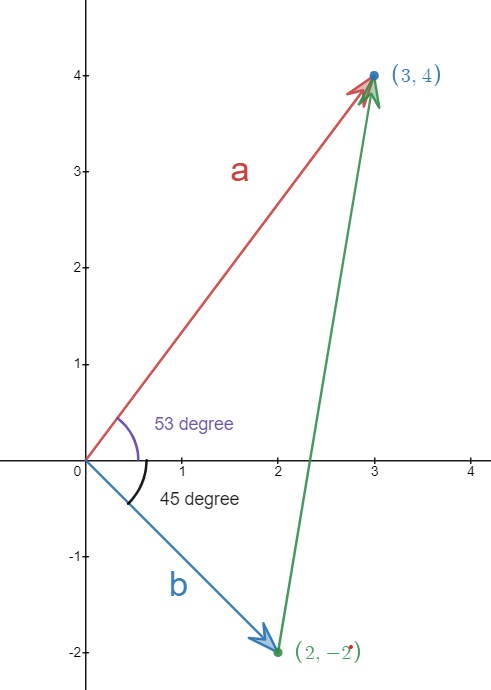
then we use cosine law:
To get the angle, we can first use sine law to get the angle for other two angle in the triangle:
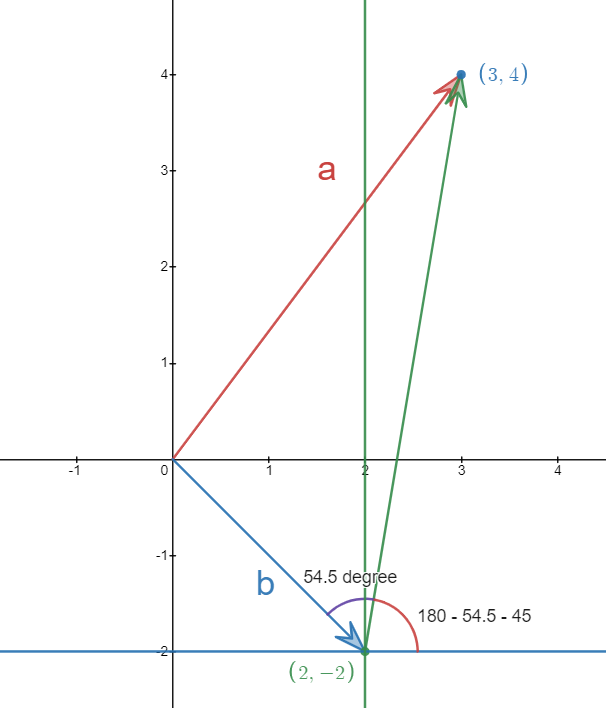
Then we can calculate the angle between \(\vec{a}-\vec{b}\) and the horizontal line:
(c) compare your result from part(a) and part(b). Ask yourself which one you prefer.
There is no need to tell which one is easier. In practice, if we have chance to put vector in coordinate, we always do that first.
- You are play chess on a 2d Cartesian plane. Say your knight is located at the corner of the chess board(the origin) and there is a juicy queen sitting at (6,8). Reminder: The knight’s movement is unique: it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L).

(a) Let’s assume your opponent is quite dumb, so he just don’t like to move the queen. Now how do you move your knight to kill the queen?
There are multiple ways to do this, here I will only show one way:
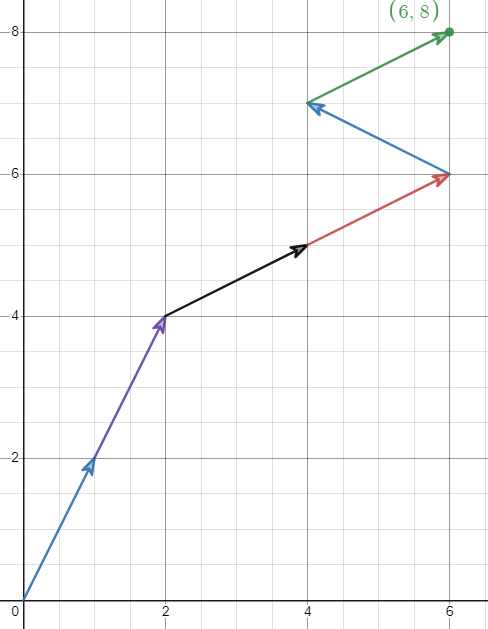
(b) We can use the vector notation to explain the movement of knight. For example, if we want to move the knight to (3,3), we can do:
Now, rewrite your result from (a) using vector addition and scalar multiplication.
This is also fairly straightforward, just read the vector from your graph and write them down as a collection of vectors:
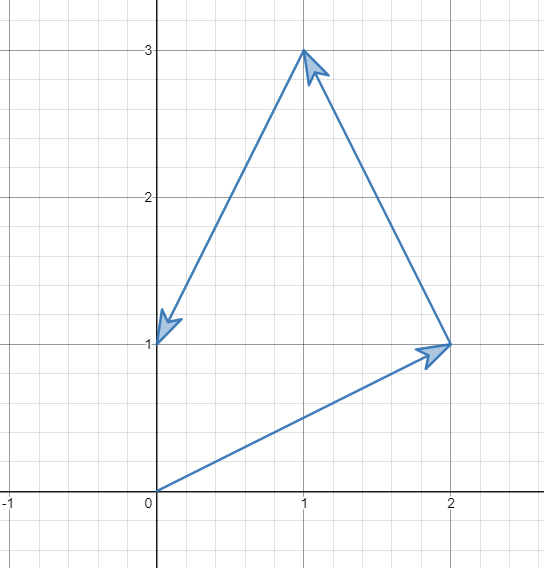
(c) Can you prove that knight can go to any location on the chess board?
To prove the knight can go to any location, we have to design a path for any location (a,b). One way to do this is to find a path for the knight to go to (1,0), then repeat it a times to get to the position (a,0). After that, find a path for the knight to go to (0,1), then repeat it b times to get to the position (a,b). the below diagram shows how to jump to (1,0) and (0,1) respectively.