Last time, we focused on the matrix in linear systems. By treating the linear equations as a transformation of vectors, we can easily predict the number of solutions. But when we tried to solve the system, we still have to do elimination. So, can we do better?
Let’s look at our equation in matrix form:
The thing we are trying to solve is \(\pmb{\color{red}x}\), and we know the transformation \(A\) and the target vector \(b\). Assume you solved the equation and you have exactly one solution, you know that the null space of this transformation is zero. In another word, the system will always give you a unique \( \pmb{\color{red}x}\) for any vector \(\pmb{b}\). But the problem is, when we change the vector \(\pmb{b}\), we have to solve the system again, and that is not good for us.
So, is there a better way to solve this?
Let’s look at the simplest equation that we all learned in elementary school:
Notice that \(a\) and \(b\) are just numbers. To solve x, we just divide the \(a\) on both side. The good thing about this is that no matter how b change, we always divide the number \(a\) to get our solution for \(\color{red}x\).
But wait for a second, we don’t have the division in matrix! Obviously, you can’t divide matrices, it doesn’t make any sense! Or is it?
The matrix act as a transformation “function”, like \( y = sin(x)\), you can’t just divide functions. But, we can change our “division” into the multiplication of the reciprocal! What is the “reciprocal” of a function? Well, it is called the inverse of function:
So how do we solve the equation? Let’s first see how we did it in function:
Assume there exist the “inverse” of matrix, we can perform the same thing as we did in function:
So what has to be true for this “inverse” in order to make the above idea practical?
It is not hard to see that the second line has to be the definition for inverse matrix:
If you treat the two matrices \(A^{-1}A\) as one matrix, Let’s call it \(I\), what is \(I\) transformation looks like?
Well, this matrix has to transform vector \({\color{red}x}\) into itself. Such transformation is called the identity matrix. Let’s construct the identity matrix together.
First, what is the dimension of this matrix? If the vector has to transform to itself, then the matrix must have size of n by n, where n is the dimension of that vector. How about the entries? The basis of this transformation should remain the same:
For example, a 3 by 3 identity matrix should looks like this:
Now we know what matrix are we looking for, it is time to see how to compute the inverse matrix.
Our goal is to find a matrix \(A^{-1}\)such that \(A^{-1}A = I\), Here we will introduce one of the methods to compute the inverse. For now, let’s accept the fact that this method works. Later on, we will find out why this method works.
The method we will use is called Gauss–Jordan elimination, a variation of the classic Gaussian elimination. Let’s say we want to find the inverse matrix of the following matrix A:
First, we have to take a look at the matrix, because not all matrices have an inverse. There are two things we need to check: First is the size of this matrix, it has to be a square matrix (2 by 2, 3 by 3, etc.). Second, it has to have linear independent rows. Or use the concepts we learned earlier, for a \(n \times n\) matrix, the dimension of column space has to be n.
For this easy example, we can see that both conditions are satisfied. So we know that this matrix has an inverse, and now we can compute it.
The first step is to write an augmented matrix by combining the matrix A and the identity matrix with the same size:
Then we do Gaussian elimination. The goal is to make the left part of the augmented matrix be identity matrix so the right part, which is the identity matrix at the beginning, will become the inverse matrix.
Let’s get started:
So the inverse of matrix \(A\) is:
We can check it by multiplying \(A^{-1}\) and \(A\):
For \(3 \times 3\) or higher dimension matrix, finding inverse can be really tedious. There are other ways to compute the inverse of a matrix, but if you do it by hand, Gaussian elimination is the most efficient one.
Now we successfully find the inverse of our matrix, we can finally find the nontrivial solution for our equation \(A\pmb{\color{red}x} = \pmb{b}\) for any \(\pmb{b}\) we want.
But you might want to ask this question: There are cases that we don’t get any solution or get infinite many solutions, so if our solution is given by a simple multiplication:
Then how can there be infinite many solutions or no solutions? An easy answer to this question is: For those cases, we couldn’t find any inverse.
To see that, we have to treat the inverse matrix as a linear transformation. Not all matrices have an inverse, for example, any matrix has different numbers of rows and columns cannot have an inverse.
Let’s look at a specific example:
Apparently, the matrix \(A\) multiply by the matrix \(B\) gives you an identity matrix, but can you say that the inverse of \(B\) is \(A\)? Sort of, but not quite. We can call them left inverse or right inverse. To be an inverse matrix, multiplying from left to right or right to left has to return the same identity matrix.
For the above example, we can easily see that:
How about the matrix that transforms 2d space to 1d line?
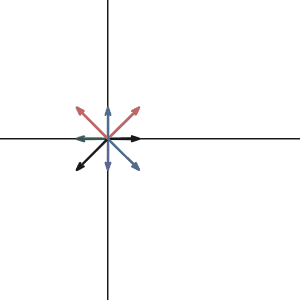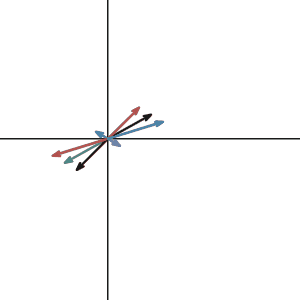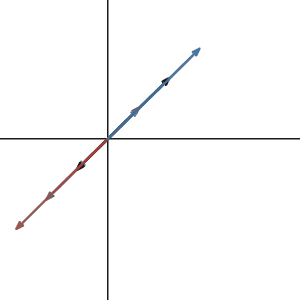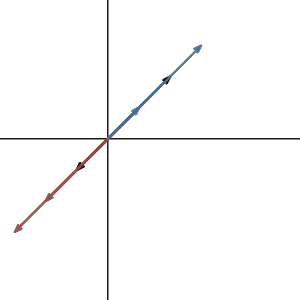
Do they have an inverse? Again, no. The inverse matrix is like the reverse operation of the previous transformation. If the transformation maps the plane to line, the reverse operation must transform a line to a plane. Which means that for a single vector on the line, it has to transform to many different vectors on the plane.
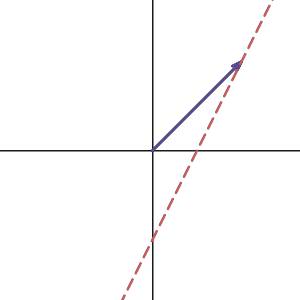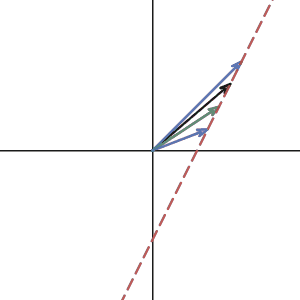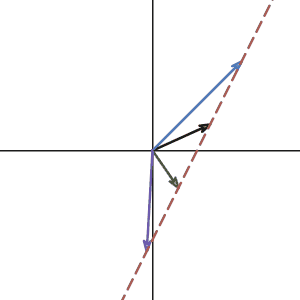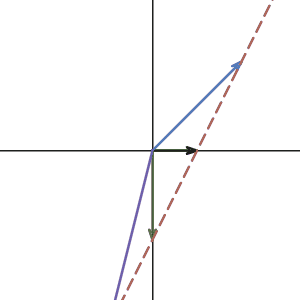
That is not a linear transformation can do. It’s like functions, for one x value, you can only get one y value. So for one vector input, you can only get one vector output.
In practice, we will see that finding the inverse in order to solve the linear system is actually not very convenient. Nowadays, computers use other methods like LU decomposition, which is so much faster than finding the inverse. Nevertheless, to have a unique solution, having an inverse matrix is a must.