As we just learned from the last section, we can create a new vector by linearly combining other vectors. But why do need this tool at all?
Let’s go back to the beginning. Before we learn any linear algebra, we mentioned the lines in three-dimension space. We find that describing lines in 2d Cartesian plane is much easier than doing the same thing in 3d space. So can we find a new way to describe lines, planes, or even space using linear combination?
Of course! But there is one thing we need to consider. The linear combination of vectors will only give you another vector, but we want more than just one vector.
For example, if I have a vector in 2d plane:
if we do a linear combination of only this vector, we can get a new vector by scalar multiplication:
we can do this for other numbers too, but you will see that no matter how you change the number, you will always end up with the vector on the same line.

If you collect all the possible linear combinations, you will just get a line.
In linear algebra, we have a specific name for such a collection of vectors: The span of vector (2,1)
Now, let’s see what can we get if we span two vector. For example, the span of vector (1,0) and (0,1). You will soon realize that one can easily get any vector in 2d plane by linear combining (1,0) and (0,1):
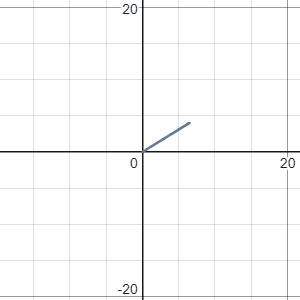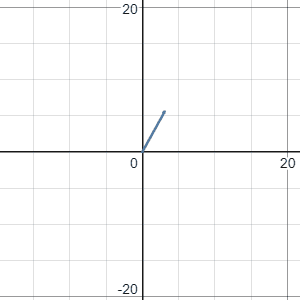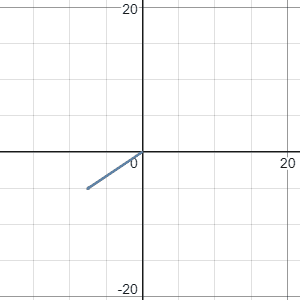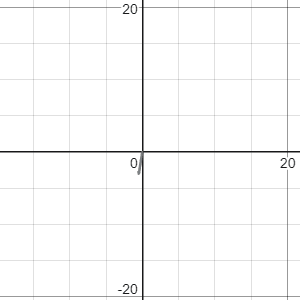
So, the span of vector (1,0) and (0,1) will give you the whole 2d plane.
You can imaging that if we graph the span of more vectors, we can end up with any multidimensional space.
For example, to describe a three dimension space, we can pick three vectors lying in the space:
To get any vector lying in the space, we can do a linear combination of the three vector:
What if we span only two vectors in 3d space? Well, just like what happens in 2d plane, most of the time, we will also get a plane in 2d space.
But, what if we span two colinear vectors? If we look at the image above, we can see that spanning vector (1,2) and the same direction vector (2,4) will not give you a whole plane. All the linear combinations of these two vectors will just sit on the same line.
So, spanning two vectors will not always give you 2d plane, sometimes it could be a line, sometime even just a zero vector.
Now you might ask: if I want to span two vectors to get a plane, or I want to span three vectors to get a 3d space, how should I select my vectors? This question is fairly easy to answer in 2d: just don’t pick the vectors that sit on the same line. But we need a better answer when we raise the dimension.
In short, we want to have all the vectors to be “unique”, which means they were not the linear combination of other vectors. Of course, we have another fancy name for this kind of vector: we call them “Linear Independent vectors”.
For example:
In 2d, There is no way you can linearly combine (1,0) to get (0,1), so they are linear independent. But you cannot say that (0,1) and (0,4) are linearly independent vectors because you can write (0,4) to be a linear combination of vector (0,1):
If that is the case, we call them “Linear Dependent vectors”.
In 3d, things are getting a little more complicated, because finding one vector is the linear combination of the other two algebraically is not easy. So, we need more useful tools to calculate. However, we can see what happens when we have one vector is the linear combination of the other two in 3d space. Let’s look at the graph below:
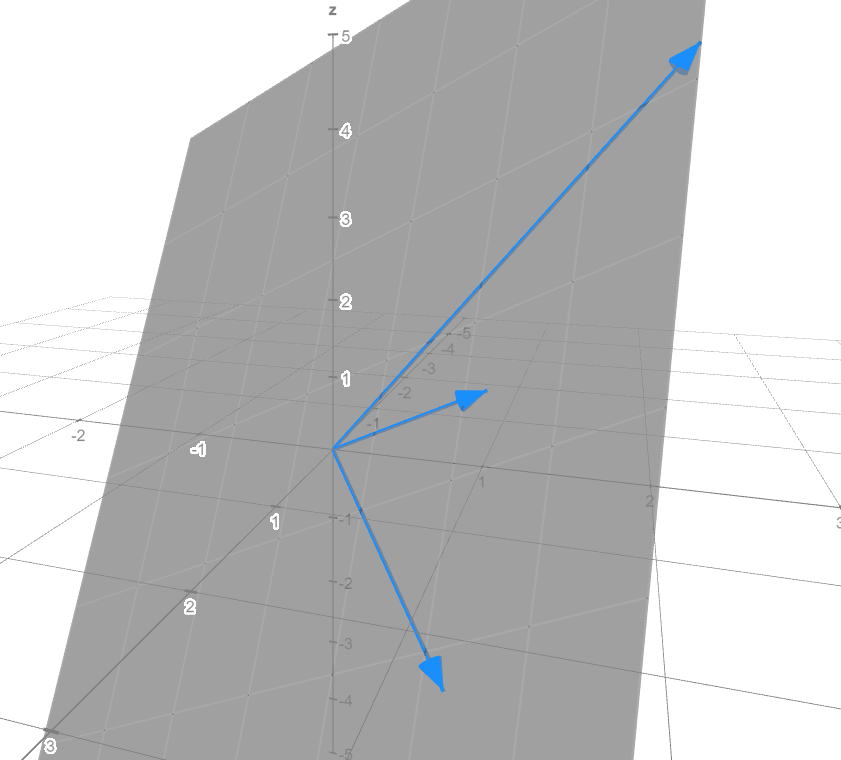
The vectors shown above are:
To proof one vector is the linear combination of other two, we can rewrite \(\pmb{v}_1\) as :
Unlike the colinear vector in 2d space, the linear independent vector in 3d can be visualized as the vector that sits on the plane spanned by the other two vectors.