Last time, we learned a special vector for linear transformation: Eigenvector. But, there are two questions we didn’t answer.
One, Is there always eigenvector and eigenvalues for matrices?
Second, How do we calculate them?
Let’s start from the definition of eigenvector and eigenvalue:
If this equation hold for some vector \(\pmb{x}\) and non-zero value \(\lambda\), then great! We found the eigenvector and eigenvalues for that matrix.
To solve this, let’s try to move all the terms on one side:
Notice that we only know the matrix \(A\), so we need some way to combine these two terms. Factoring out vector \(\pmb{x}\) seems to be a good idea, but is there any way to factor out the vector \(\pmb{x}\)?
Yes! We know the fact that for the square matrix with the same size:
So if we can rewrite number \(\lambda\) into a matrix with the same size as \(A\), then we can combine the matrices and factor out \(\pmb{x}\). But how do we rewrite numbers to a matrix? That is not hard since this number is multiplying on a vector, We can add a linear transformation that does nothing in front of vector \(\pmb{x}\):
Now, the scalar \(\lambda\) is a linear transformation \(\lambda I\), therefore, we can add the matrix \(A\) and the new matrix \(\lambda I\):
The new matrix \((A- \lambda I)\) multiply some vector \(\pmb{x}\) gives you zero vector. How do we find the vector \(\pmb{x}\)? Easy! This is just asking you to find the null space of matrix \((A- \lambda I)\)!
Before, to find null space, we need to solve the linear system \(A\pmb{x} = 0\). But in our case, the matrix itself has some unknown variable in it, which is the number \(\lambda\). So how could we find the null space of an unknown matrix?
Here we will introduce a technique that we didn’t mention before, call determinant. In short, the determinant calculates the ratio between the size of space before and after the linear transformation. In 2d, it is simply the ratio between the area before and after the linear transformation. To calculate determinant for any \(2\times2\) matrix, we just need to do:
We are not going to cover the method of finding \(3\times3\) or higher dimension matrix’s determinant in this chapter. Feel free to search them up and think about why.
Why is finding the ratio of areas useful in our case? Because if a non-zero null space exists for a matrix, the determinant of this matrix must be zero.
Why? By the rank-nullity theorem, if null space has the dimension greater than zero, it means our rank is less than the dimension of matrix. So the linear transformation will transform the space to a space with lower dimension.
If the matrix is \(2\times2\) but the rank is lower than 2, for example, is 1. It just means the matrix will transform any 2d vector to a 2d vector on a line (1d). So what will be the ratio of areas before and after the transformation? Obviously is zero(The whole 2d plane was “smashed” into a line).
Great! Now is time to put everything together and calculate some eigenvalue & eigenvector! Let’s find the eigenvalue & eigenvector for the matrix we discussed last time:
The first thing we do is to get the matrix \(A - \lambda I\):
Then, we write down the determinant of this matrix:
To solve \(\lambda\), we just need to set this expression to zero. But before we do that, look at this familiar expression! It is a quadratic! Later, you will see that the determinant of \(A - \lambda I\) will always be a polynomial. We have a special name for this: the Characteristic polynomials.
In our case, this polynomials is extremely easy to solve:
So, \(\lambda_1 = 1\) and \(\lambda_2 = 2\) are the eigenvalue of the matrix \(A\). To solve the eigenvector correspond to these eigenvalue, we just plug these back into our matrix \(A - \lambda I\) and find the null space:
To find the null space, we solve the linear system \(A\pmb{x} = 0\):
Therefore, the eigenvector corresponding to eigenvalue \(1\) is the vector
Using the same method, we can get the eigenvector for eigenvalue \(\lambda_2 = 2\) is vector
Awesome! We solved all the eigenvalue and their eigenvector. Does that mean we solved everything? Of course not. Remember, we got lucky when solving the polynomial. Let’s go back to the characteristic polynomial and see what are we missing.
The characteristic polynomial we had is \((1-\lambda )(2-\lambda)\), but in principle, we could have any polynomials. Take \(2\times2\) matrix as example, our characteristic polynomial will be a quadratic:
For our case, we ended up with two distinct \(\lambda\) values. But we could also have two same \(\lambda\) values or no real \(\lambda\).
The two same \(\lambda\) values case is not that interesting. In 2d, the transformation that has only one eigenvalue will look like a shear transformation. The interesting case is when we have no real \(\lambda\) values.
Let’s imaging: What kind of transformation in 2d that has no eigenvector? Having eigenvectors means there are some directions where all the vectors alone that direction do not change their direction after the transformation. So, having no eigenvector means all the vectors in 2d change their direction after the transformation. Did we see any of the transformations that can do this?
Of course! Any transformation that rotates the plane!
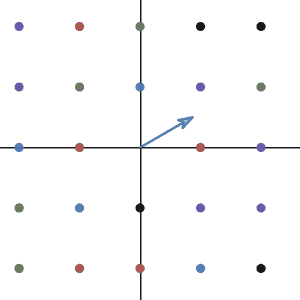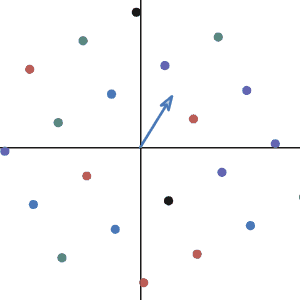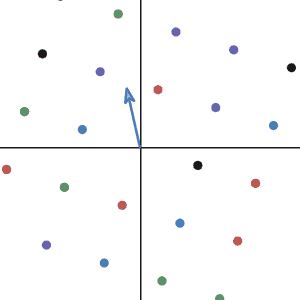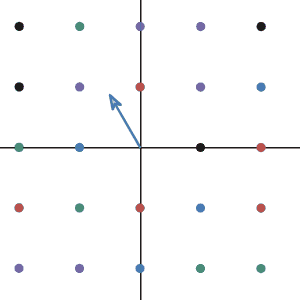
Let’s take the very first linear transformation we saw. As you can see, all the vectors do not end up in the same direction after the transformation.
If you learned the imaginary number before(don’t worry if you never learn it, but I highly recommend you check it out online if you never), you will know that the quadratic that have no real solution will have the imaginary solution. So our eigenvalue will be imaginary. In fact, imaginary eigenvalue will always has something to do with rotation. However, the imaginary eigenvalue is beyond the scope of our note.