Now comes one of the biggest applications of Matrix multiplication. Sometimes when we solve a problem, we might find that the classic Cartesian coordinate is not the best coordinate to work with. For example, let start with some random points on the Cartesian coordinate and form a line segment:
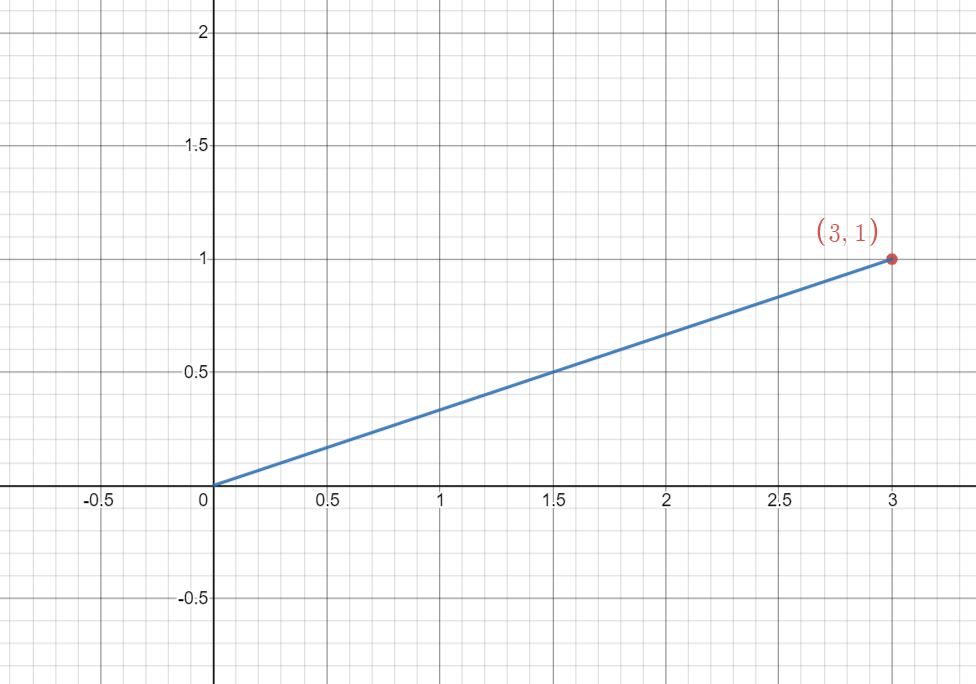
Say we want to find the tip of the bar after a rotation of 15 degrees, to do this normally takes quite a lot of work. But, if we convert the point \((3,1)\) to the polar coordinate, and then we do the rotation. After that, we can covert the transformed polar coordinate into Cartesian coordinate.
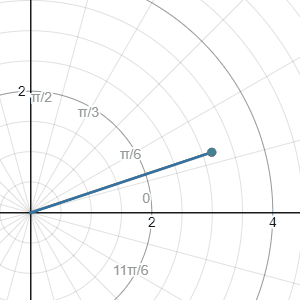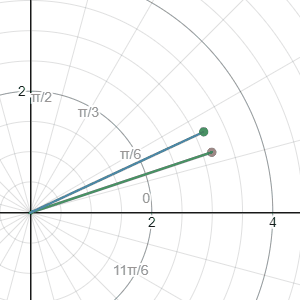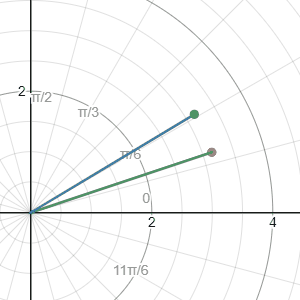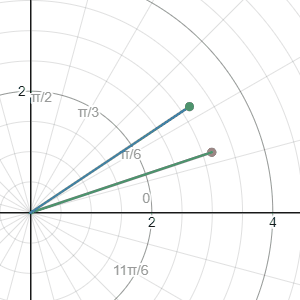
So, can we do the same in linear algebra? Can we change one vector in one coordinate(basis) to another one?
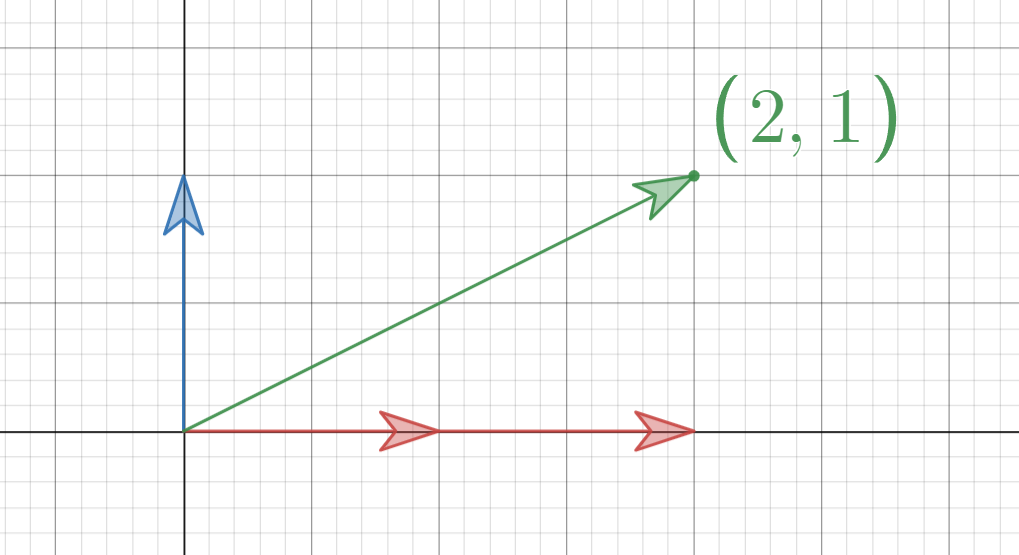
Let’s start with a vector in the classic Cartesian coordinate, pick any two numbers, let’s say \((2,1)\).
The basis of Cartesian coordinate is vector \((1,0)\) and \((0,1)\), so the meaning of vector \((2,1)\) is just two pieces of \((1,0)\) and one piece of \((0,1)\):
Here we have another 2d basis create by spanning vector \((1,1)\)and \((-1,2)\):
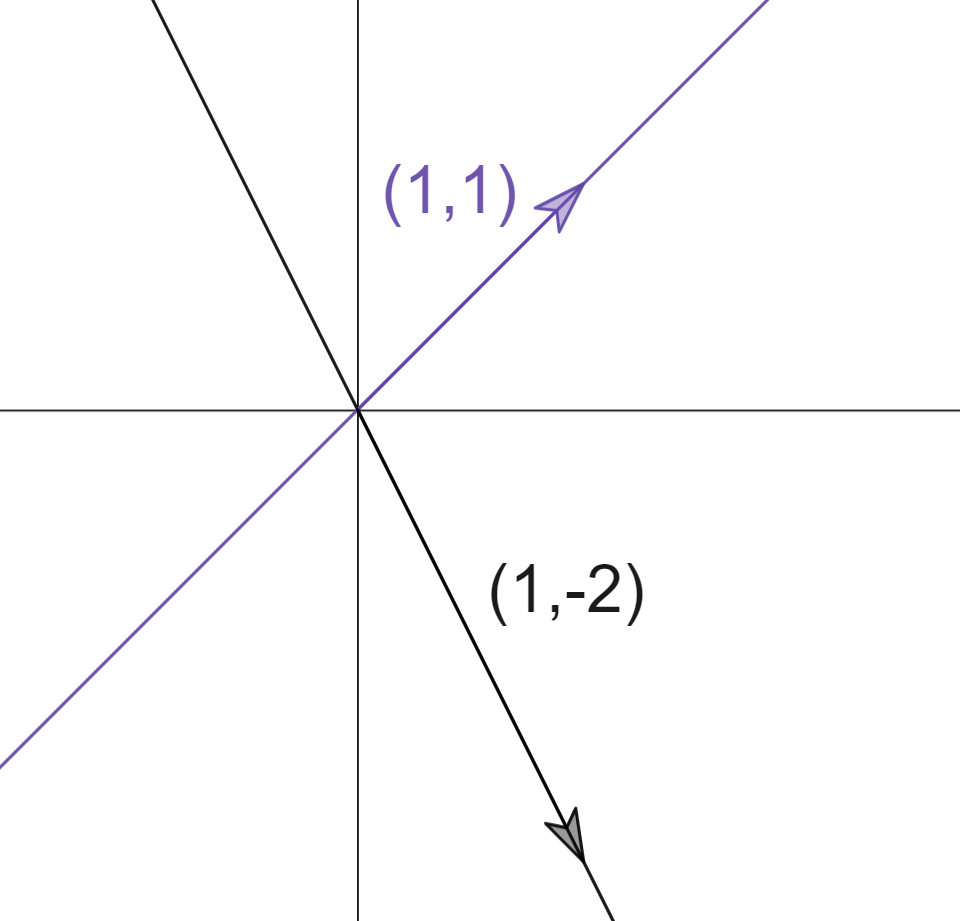
In this new basis, our vector \((\color{red}2,\color{red}1)\) will no longer looks the same as the vector \((2,1)\) in Cartesian coordinate. We can do a quick calculation to see what is \((\color{red}2,\color{red}1)\) in the new basis:
To not make you confused, I will label all the vectors lie in Cartesian coordinate black, and the vector lies in new coordinate red.
So the question is, what should be the vector \((2,1)\) in our new basis? In another word, how many \((1,1)\) and \((-1,2)\) combined together will give you \((2,1)\)?
You might find the statements here are kind of confusing, so I will help you out by showing you the solution first:
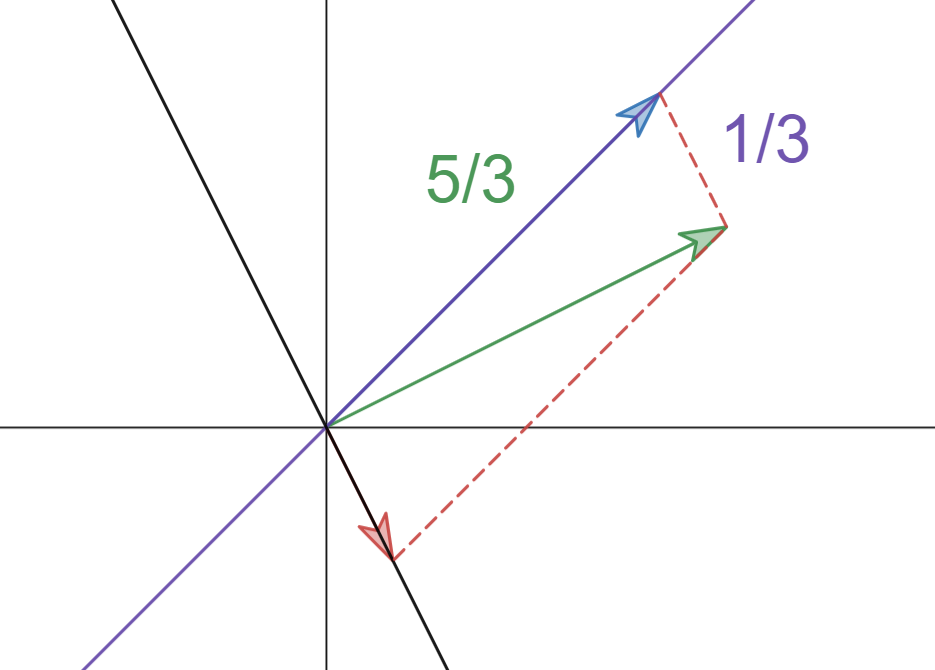
It turns out, if you take \(\color{red}{\frac{5}{3}}\) of vector \((1,1)\) and \(\color{red}{\frac{1}{3}}\) of vector \((-1,2)\), you will end up with vector \((2,1)\). So our vector \((2,1)\) in the new basis has a new name \((\color{red}{\frac{5}{3}},\color{red}{\frac{1}{3}})\).
Now how do I got these number out? Think about this, if we rewrite the above relation in a matrix form, we will have:
It looks like the matrix
can transformed our \((\color{red}{\frac{5}{3}},\color{red}{\frac{1}{3}})\) back to what it was in Cartesian coordinate. What do we want is to know what is \((2,1)\) in new basis, so we have to find the inverse:
Strange, right? To know the presentation on one specific basis, you have to apply the inverse transformation. but this is what it is.
For the previous example, the way we get \((\color{red}{\frac{5}{3}},\color{red}{\frac{1}{3}})\) is by first put our basis vector together and form the matrix
then we can find its inverse:
And the last step is to put any vector we want to transform in it and do multiplication.
Can we do it for any basis? Here is the animation I made that shows the vector \(
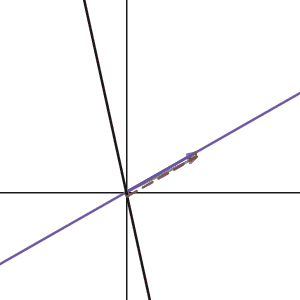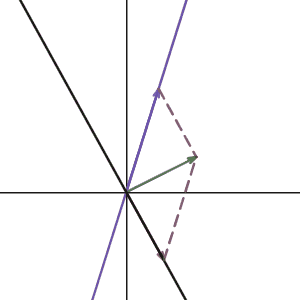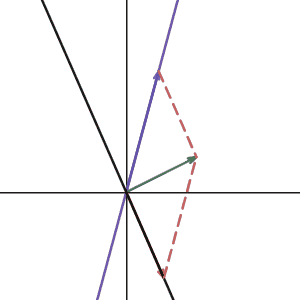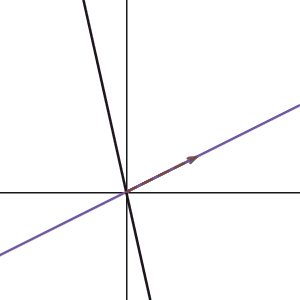
Now we know how to convert a vector on another basis, let’s do something fun here.
Assume you have some transformation \(T\) on some basis. For example, the Cartesian coordinate. The transformation \(T\) has a dimension of \(n \times n\). Let’s say we have a vector that lies in the Cartesian coordinate called \(\pmb{a}\) and if you transform that vector, you will get vector \(\pmb{b}\):
Here comes the cool part. Instead of doing this transform in the old, boring Cartesian coordinate, why not do it in a new fancy basis? The basis vectors of this new basis form a matrix \(P\). We can rewrite the vector \(\pmb{a}\) and \(\pmb{b}\) in our new basis:
We know the fact that you can use the transformation \(T\) to transform \(\pmb{a}\) to \(\pmb{b}\) but you can see that wouldn’t work in our new basis. Namely, you cannot apply the same transformation \(T\) on \(\pmb{a}'\) to give you \(\pmb{b}'\):
So we need a new “look” of our transformation \(T\) in the new basis. We shall name it \(T'\), so that:
With some simple algebra, we can get the expression of \(T'\):
We can see that the way we rewrite a transformation for the new basis is kind of different than for vectors. Memorizing the expression of \(T' = P^{-1}TP\) is not hard. Imagine you are doing business in another country. The transformation is the business process(Take some money and return some money). \(T'\) and \(T\) is just the same business process but in the different country. say one in US one in the UK. The matrix \(P\) converts one currency to another, in our case dollar to pound. So if you are American and want to do the business in the US, all you need is the transformation \(T\). But if you are a gentleman from UK, The same business process became to:
1) Convert the money to dollars (\(P\))
2) Do the business in the US (\(T\))
3) Convert the dollar you earned in the US back to pounds and enjoy your life (\(P^{-1}\))
So overall, what you did is:
and that is the process \(T'\).
Notice that what we are dealing with is the \(n \times n\) case. We can generalize this idea to any dimension, but that is not what we focus on here. Most of the time, we will be working on \(n \times n\) case, especially \(3 \times 3\) or \(4 \times 4\) for physics.